Infinite Dimensional Geometry is in the background of Riemannian Geometry on finite-dimensional manifolds. Indeed geodesics are curves that locally minimize length, and the space of curves is infinite-dimensional. However the intuition that geometers have of the finite-dimensional world is sometimes misleading...
The Universal Teichmüller Space is a infinite-dimensional Banach manifold that can be endowed with a structure of Hilbert manifold for which it has an uncountable number of connected components. This manifold is universel in the sense that it contains all the Teichmüller spaces of surfaces of genus g. It contains also the quotient space of the group of diffeomorphisms of the circle modulo the group of Möbius transformation.
A hyperkähler manifold is a smooth manifold endowed with a Riemannian metric and 3 complex structures satisfying the relations of the quaternions, with strong compatibility conditions. In finite dimensions, roughtly speaking, the tangent space of a Kähler manifold carries an hyperkähler structure, at least in a neighboorhood of the zero section. It was the goal of my PhD to construct examples of infinite-dimensional hyperkähler manifolds.
Poisson Geometry is a formalization of Hamiltonian Equations coming from Physics. It is related to the theory of Lie groups, since the dual of a Lie algebra is naturally endowed with a Poisson bracket, whose symplectic leaves are the coadjoint orbits of the corresponding Lie group. In the infinite-dimensional setting, some weird phenomena occur like the fact that a Poisson bracket may not be given by a Poisson tensor.
Shapes from Tosca Database
Shape Analysis has been developped by the need to recognize, compare, classify objects like shapes and images automatically. Infinite-dimensional Geometry comes into play as soon as one thinks of the objects as deformable, since the space of deformation of even very simple objects like a curve in the plane is infinite-dimensional. Applying tools from Differential Geometry in this area is powerfull, and leads to a lot of applications like face recognition or medical imaging.
Pictures from Assembil.com
The stretch of fabric refers to a variation of the area of fabric patches, whereas the shear refer to a deformation of a circular fabric patch into an elongated ellipse. Shear has to be minimized in the garment design process since it induces creation of disgraceful folds. Mathematically, an area-preserving map from a 2D-surface into the plane is a symplectic map, a map without shear is a conformal map, a map without stretch and shear is a map preserving the Kähler structure of the surface. Maps with controlled shear are quasi-conformal maps. They are the maps used in garment design since fabrics have elasticity. They form an infinite-dimensional manifold.
Picture by James Montaldi.
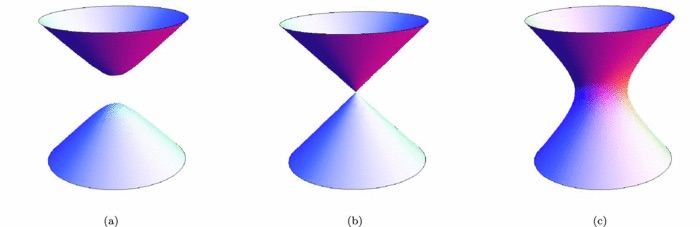
Isospectral Matrices are particular examples of Coadjoint Orbits which are obtained by the natural action of a Lie Group on its Lie algebra. Coadjoint orbits of compact Lie groups are Kähler manifolds, whereas their complexifications are hyperkähler manifolds.
For a coffee break, I invite you to read this beautiful paper by Alexander Belyaev : Plane and Space Curves. Curvature. Curvature-based Features.